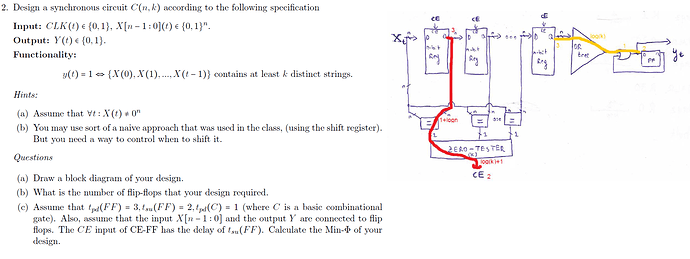
Handout 11 - Q2

Handouts and Homeworks
1

Some things regarding Handout 11 Q2:

Here is the question and the attached solution which was posted

Handout11_Q2
Handout11_Q21887×711 306 KB

  1. How is the design correct if we get an input vector which is not different? It seems like will then still get y=1 rather than y=0

  2. How many registers are there in here? Because if there is one for every time iteration then that makes no sense since that means the amount changes over time and what is sketched here is just not something I can actually design

  3. The delay path is marked in red. How is that the longest path if it does not start with an input and ends with an output?

2

  1. Notice the use of CE, we only read in a new string if its different from all the ones we saved before.

  2. There are k-1 n-bit registers (you can see it by looking at the zero testers size), and another FF at the end. That makes a total of n(k-1)+1 FF in the design.

  3. The delay of a synchronous circuit is defined as the largest time from an input or a FF output port to an output or a FF input port. This can be explained by the simulation algorithm, where for every clock cycle it treats every FF as a set of new input and output gates.

3

Regarding 1: But how does that give a y=0 output if CE=0?
Regarding 3: Is this a topic we covered in class/rec.? There was a whole part related to this we skipped over as far as I understand. Unlike the delay of comb. circuits it seems like we glossed over this. (I am not referring to delay in general or the SIM algorithm)

4

  1. All registers are set to contain the all zeros string at the start of the simulation. As long as there havn’t been k different strings, the right-most register will retain that value, thanks to the CE input. When the k’th different string is entered, the right-most register will hold one of the strings (that is guaranteed to be different from the all zeros string), so the OR-Tree will return a 1.

  2. I’m not sure I understand your question. The topic was covered in both the lecture and the recitation. The part we “skipped over” is Timing analysis (which we briefly discussed when we talked about t_pd and t_cont of a circuit).